Run XBMC Fullscreen on second monitor in Ubuntu

After trying to find a way to run XBMC fullscreen in second monitor I decided a bespoke solution was the way forward.

UPDATE: This post was written back in the times of Ubuntu 12 (I think). As such as as you can see from the comments at the bottom of the post there are now better ways of accomplishing this task.

Although this tutorial focuses on the XBMC Media Center it can be applied to many other programs.

I know there have been work-arounds for previous versions of Ubuntu but over the years they have fallen by the wayside.

What I’m going to show you now will allow you to run XBMC fullscreen in second monitor.

Points to Note

1. If you want to copy the code I advise you to click on the word “bash” above the code, this will open up a new box for you to copy the correct code from
2. This tutorial is to get XBMC running in fullscreen but the code can be used to get many other programs running in fullscreen
3. I have structured the tutorial so that you can run XBMC fullscreen in second monitor but you can easily alter the code to have it fullscreen in your primary monitor
4. Quiet a bit of this tutorial uses the terminal, you can open a Terminal window by pressing control (or command for MacOS), Alt & T at the same time

 

Step 1: Run XMBC and get the title

Run XBMC up so that we can find the title it uses.

To find the title type

wmctrl -l

into the terminal. This will bring up a list of windows that the window controller is in charge of.

The chances are that the XBMC window is called “XBMC Media Center” but it may be different on yours so look in the last column of the output and copy the XBMC title.

 

Step 2: compizConfig settings manager

See if you have compizConfig installed by typing

which ccsm

If you get a path to the executable such as

/usr/bin/ccsm

then you have it installed. If not type

sudo apt-get install compizconfig-settings-manager

Now you can start the program by entering

ccsm

in the terminal window.

 

Once the program has loaded look on the right hand side and under “Effects” click “Window Decoration”

Now find the field titled “Decoration windows” and click on the green plus icon on the right hand side.

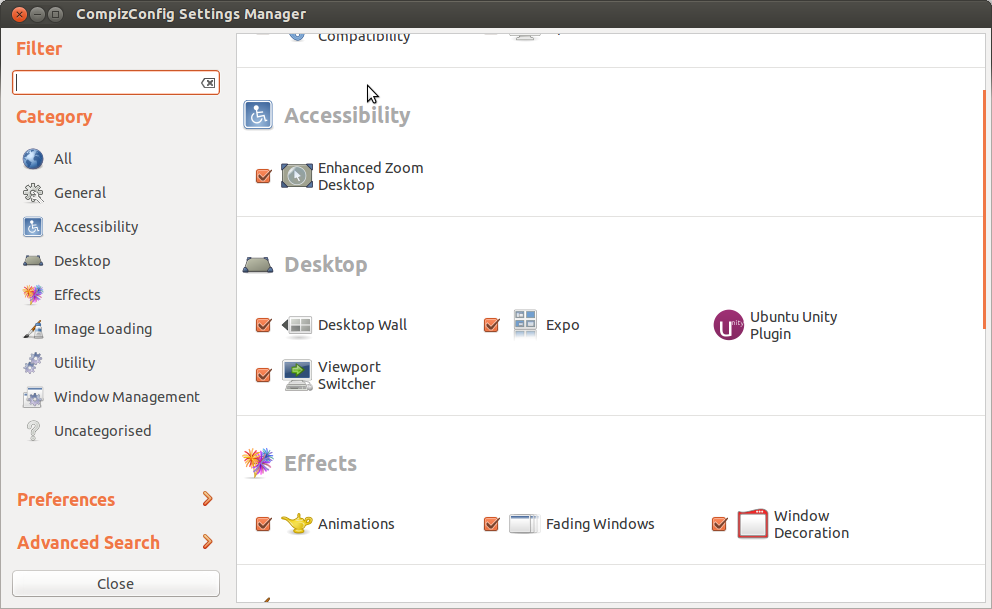
In the first drop down box select “Window Title”

In the second box enter the title that the previous step displayed

Click the “Invert” checkbox and click Add

Once that box disappears you can exit that program.

What this does is hide the title bar from from the XBMC window

 

Step 3: Get your display information

Now we need to get the display details

Run xrandr from the terminal

xrandr | grep " connected" | sed -e 's/\(.*\) connected \(.*\) (.*/\nDisplay Name: \1\nDisplay Sizes: \2 /'

You will be presented with an output similar to the following

Display Name: VGA-0
Display Sizes: 1440x900+0+0

Display Name: DVI-I-1
Display Sizes: 1680×1050+1440+0

Assuming you’re wanting the program in your second monitor then we the information from the latter of the two monitors

The display name is straight forward – take a note of this.
The next line not to straight forward. The value is made up of

display-width x display-height + start-x-pxs-from-the-left + start-x-pxs-from-the-top

The value we need here is the third value as this will be where the XBMC window will start (from the left)

 

Step 3: Create out actual script file

Create a file called….well, what ever you want, I called mine XBMC_fullscreen.sh

In this file type or paste the following:

#!/bin/bash

# This script will run a program in fullscreen mode (no borders or
# title bar etc) on a second monitor. It can used for many programs
# and on either the primary or secondary monitor

#This is the executable file or path
PROGRAM='xbmc'

# This is the output of wmctrl -l for the program that we are using
NAME='XBMC Media Center'

# This is the device name of the monitor we want to display the program on
DEVICE='DVI-I-1'

# If you want the program to be fullscreen on your second monitor
# this variable should be the width of your primary monitor
PRIMARYWIDTH=1440

# Run the program , then wait a bit before carrying on
    # If your program doesn't load in time then try increasing this value
$PROGRAM > /dev/null 2> /dev/null & disown && sleep 3

## Set the Open GL environment variables
# Set the vertical blanking to on
__GL_SYNC_TO_VBLANK=1
# And make sure OpenGL syncs the correct monitor
__GL_SYNC_DISPLAY_DEVICE="$DEVICE"

# Do we want a screensaver
SDL_VIDEO_ALLOW_SCREENSAVER=0

# Set the dimensions of the program in the monitor
wmctrl -r "$NAME" -e '0,'$PRIMARYWIDTH',-1,-1,-1'

# Maximize it
wmctrl -r "$NAME" -b toggle,fullscreen,maximized_vert

 

Now you need to change the NAME variable to something other than the default value **IF** your version of XBMC has a different title in the window (see last step).

You also need to change the DEVICE variable to the one returned as Display Name above.
Lastly you need to change the PRIMARYWIDTH variable to the third number in the returned Display Sizes above.

Now let’s take a look at what this does (just the important lines though)

#!/bin/bash

This tells the system to use bash to execute the script

PROGRAM='xbmc'

Set the program to the path we found earlier

NAME='XBMC Media Center'

This sets the title of the the window that we want to control

DEVICE='DVI-I-1'

This is the name of the display device that we noted down earlier

PRIMARYWIDTH='1440'

This is the width of your primary monitor

$PROGRAM > /dev/null 2> /dev/null & disown && sleep 3

Ok, this line will:

1. Start the program
2. Redirect the output
3. Disown the process so that the the script can carry on
4. Wait 3 seconds so the program has a chance to start

__GL_SYNC_TO_VBLANK=1

Set the vertical line blanking to on

__GL_SYNC_DISPLAY_DEVICE="$DEVICE"

Make sure that we tie our XBMC window to the device we want

SDL_VIDEO_ALLOW_SCREENSAVER=0

Make sure we don’t have the screensaver

wmctrl -r "$\$NAME" -e '0,"$PRIMARYWIDTH",-1,-1,-1'

This will set the window to start at the end of the primary monitor

wmctrl -r "$\$NAME" -b toggle,fullscreen,maximized_vert

This will put the window in full screen but we also need to maximize the window vertically

 

Step 5: Save the file

Now we need to save the file and make it executable.

I’m sure you know how to save a file but then once it’s saved go back into the terminal and type

chmod +x

So for me it was

chmod +x ~/xbmc_fullscreen.sh

Step 6: Create a shortcut

If you haven’t already got it, install gnome-panel

sudo apt-get install --no-install-recommends gnome-panel

Now type

gnome-desktop-item-edit ~/Desktop/ --create-new

This will bring up a box that will enable us to add a shortcut to the desktop. We can then drag and drop it on the launcher.

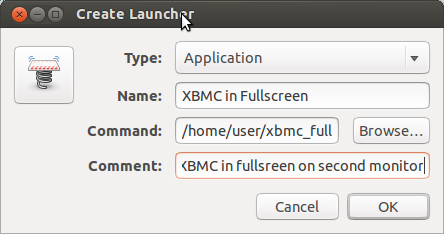
Ok, so

In the “Type” box leave the default value (Application)

In Name type anything you like, I typed “Run XBMC in Full Screen”

In the 3rd box type the path to our shell file in the form of /home/user/xbmc_fullscreen.sh

If you want to type any comments in the last box then feel free.

Take a look on your Desktop and you should now have a shortcut to XBMC that works as default in full screen.

If you want, simply drag this shortcut over the launcher to the side of the screen.

That about does it for this script.

That’s it, thanks for looking, I hope you enjoyed the post and don’t forget to leave your comments below.

Update

At some point further down the line the above script stopped working for me. It appears as if it needed a bit of a timeout so I often had to run a script containing these commands. This basically goes through the previous proceedure but as the XBMC program is already running it just sets the GUI co-ords etc.


PROGRAM='XBMC'
NAME='XBMC Media Center'
DEVICE='DVI-I-1'
PRIMARYWIDTH=1440
__GL_SYNC_TO_VBLANK=1
__GL_SYNC_DISPLAY_DEVICE="$DEVICE"
SDL_VIDEO_ALLOW_SCREENSAVER=0
wmctrl -r "$NAME" -e '0, '$PRIMARYWIDTH',-1,-1,-1'
wmctrl -r "$NAME" -b toggle,fullscreen,maximized_vert


If you have run the first part of the post but XBMC is still in your primary monitor then try this part. Hopefully your system just needed a bit of a timeout before the wmctrl commands were set.